The electronic structure gives the probability to find an electron at a certain location. Computation of electronic structures is a fundamental operation needed in physics, chemistry, and materials science. One important example is the computation of potential energy surfaces needed for numerical quantum dynamics calculations. We use the Hartree-Fock and Density Functional Theory (DFT) methods. DFT currently provides the best compromise between computational cost and accuracy for many applications and the Hartree-Fock method is used as a starting point for more accurate methods such as Configuration Interaction and Coupled Cluster methods. However, already at the Hartree-Fock/Density Functional Theory level calculations of electronic structures are very demanding in terms of computer resources. In this project the aim is to reduce the computational cost and better utilize available computer resources. We pursue this goal following two main lines of action.

Linear scaling

Traditional algorithms used in Hartree-Fock and Density Functional Theory calculations exhibit poor computational complexity. That is, a two-fold increase of the number of electrons in the system generally leads to an eight-fold increase in processor time and a four-fold increase of the memory usage needed to solve the problem. Therefore, our first line of action is to reduce the computational complexity to linear complexity. Our work on linear scaling methods has focused on efficient computation of the entries of effective Hamiltonian matrices [4], calculation of the electron density matrix [2,5], as well as analysis and development of methods to bring about matrix sparsity [3]. An important part of our research concerns the combination of linear scaling algorithms into a complete program using sparse data structures at all times [1,4]. In this way the complexity is reduced to linear, both in processor time and memory usage.

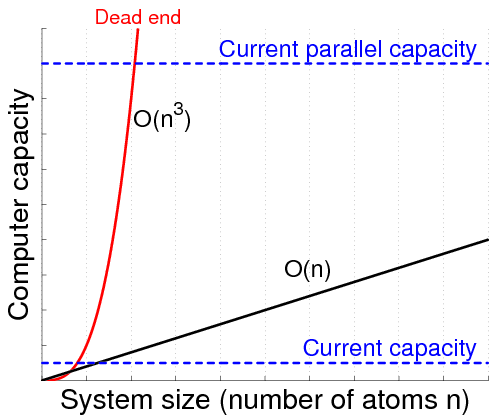
Parallelization

The second line of action regards the parallelization of the code. The parallel code should utilize all levels of parallelism available on the system, from instruction level parallelism to parallelization for distributed memory. To do this, the Chunks & Tasks framework will be used. Using this framework allows for designing algorithms without explicitly specifying which processor or computation node that should perform a certain part of the computation or how data is communicated. All such aspects are handled by the general Chunks & Tasks framework.

Implementation

Developed algorithms are implemented in the Ergo quantum chemistry program (www.ergoscf.org). Ergo is currently parallelized for shared memory using OpenMP and POSIX threads.

References

1. Nonmonotonic recursive polynomial expansions for linear scaling calculation of the density matrix. Emanuel H. Rubensson. In Journal of Chemical Theory and Computation, volume 7, pp 1233-1236, 2011. (DOI).
2. Methods for Hartree–Fock and density functional theory electronic structure calculations with linearly scaling processor time and memory usage. Emanuel H. Rubensson, Elias Rudberg, and Pawel Salek. In Linear-Scaling Techniques in Computational Chemistry and Physics: Methods and Applications, pp 263-300, Springer, Dordrecht, The Netherlands, 2011. (DOI).
3. Assessment of density matrix methods for linear scaling electronic structure calculations. Elias Rudberg and Emanuel H. Rubensson. In Journal of Physics: Condensed Matter, volume 23, pp 075502:1-10, 2011. (DOI).
4. Bringing about matrix sparsity in linear-scaling electronic structure calculations. Emanuel H. Rubensson and Elias Rudberg. In Journal of Computational Chemistry, volume 32, pp 1411-1423, 2011. (DOI).
5. Kohn–Sham density functional theory electronic structure calculations with linearly scaling computational time and memory usage. Elias Rudberg, Emanuel H. Rubensson, and Pawel Salek. In Journal of Chemical Theory and Computation, volume 7, pp 340-350, 2011. (DOI).

Back